Deep learning models are based on activation functions that provide non-linearity and enable the network to learn complex patterns. This article will discuss the SoftPlus activation function, what it is, and how it can be used in PyTorch. SoftPlus can be said to be a naive form of the popular ReLU activation, which mitigates the shortcomings of ReLU but introduces its own shortcomings. We’ll discuss what SoftPlus is, its mathematical formula, how it compares with ReLU, what its advantages and limitations are, and take a look at some PyTorch code that uses it.
What is SoftPlus activation function?
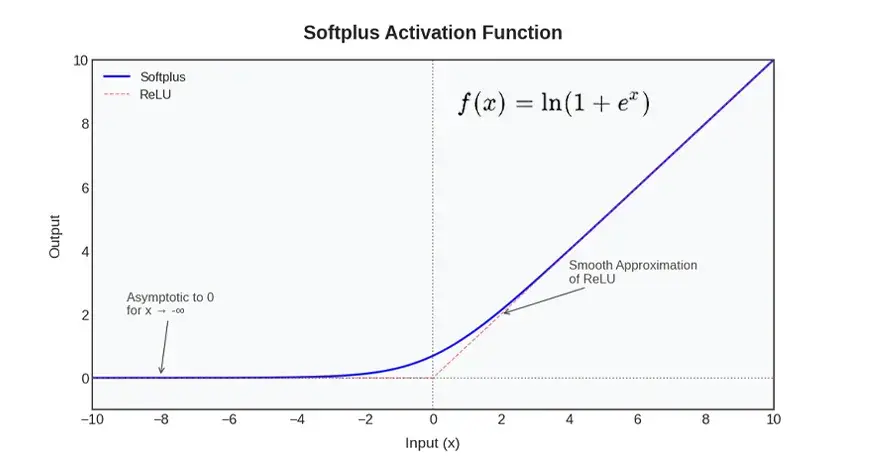
The SoftPlus activation function is a non-linear function of neural networks and is characterized by a smooth approximation of the ReLU function. In simple words, SoftPlus acts like ReLU in cases when the positive or negative input is very large, but a sharp corner at the zero point is absent. Instead, it grows smoothly and produces marginally positive outputs for negative inputs rather than a fixed zero. This continuous and differentiable behavior shows that SoftPlus is continuous and differentiable everywhere, unlike ReLU, which is discontinuous (with a sharp change in slope) at x = 0.
Why is SoftPlus used?
SoftPlus is chosen by developers who prefer to provide more convenient activation. Even non-zero gradients where ReLU would otherwise be inactive. The gradient-based optimization avoids the large perturbations caused by the smoothness of SoftPlus (the gradient is changing smoothly rather than moving forward). It naturally clips the output (as does ReLU) yet the clipping is not zero. In short, SoftPlus is a soft version of ReLU: It is like ReLU when the value is large but better around zero and is nice and smooth.
SoftPlus Mathematical Formula
SoftPlus is defined mathematically as:
When? x is big, Ex is very large and therefore, ln(1 + ex, very similar to ln(ex,equal to xThis implies that SoftPlus is approximately linear on large inputs like ReLU,
When? x is big and negative, Ex Thus, is very small ln(1 + ex, is approximately ln(1)And this is 0. The values produced by SoftPlus are close to zero but never zero. To take the value zero, x must approach negative infinity.
Another thing that is useful is that the derivative of SoftPlus is sigmoid. derivative of ln(1 + ex, Is:
Ex / (1 + ex,
This is the sigmoid of xThis implies that at any instant, the slope of the softplus is sigmoid(x)That is, it has a non-zero gradient everywhere and is smooth. This makes SoftPlus useful in gradient-based learning because it does not have flat regions where gradients vanish.
Using SoftPlus in PyTorch
PyTorch activation provides Softplus as a native activation and thus can be easily used like ReLU or any other activation. Two simple examples are given below. The former uses SoftPlus on a small number of test values, and the latter demonstrates how to incorporate SoftPlus into a small neural network.
softplus on sample input
The snippet below applies nn.Softplus For a small tensor so you can see how it behaves with negative, zero and positive inputs.
import torch
import torch.nn as nn
# Create the Softplus activation
softplus = nn.Softplus() # default beta=1, threshold=20
# Sample inputs
x = torch.tensor((-2.0, -1.0, 0.0, 1.0, 2.0))
y = softplus(x)
print("Input:", x.tolist())
print("Softplus output:", y.tolist())
What it shows:
- At x = -2 and x = -1, the value of softplus is a small positive value instead of 0.
- The output at x =0 is approximately 0.6931, i.e. ln(2)
- In the case of positive inputs like 1 or 2, the results are slightly larger than the input because SoftPlus smoothes the curve. SoftPlus is approaching increasing x.
PyTorch’s softplus is represented by the formula ln(1 + exp(btax))Its internal limit value is 20 to prevent numerical overflow, SoftPlus is linear in large betas, which means that in the case of PyTorch returns are just x,
Using SoftPlus in Neural Networks
Here is a simple PyTorch network that uses Softplus as the activation of its hidden layer.
import torch
import torch.nn as nn
class SimpleNet(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.activation = nn.Softplus()
self.fc2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = self.fc1(x)
x = self.activation(x) # apply Softplus
x = self.fc2(x)
return x
# Create the model
model = SimpleNet(input_size=4, hidden_size=3, output_size=1)
print(model)
Passing inputs through the model works normally:
x_input = torch.randn(2, 4) # batch of 2 samples
y_output = model(x_input)
print("Input:n", x_input)
print("Output:n", y_output)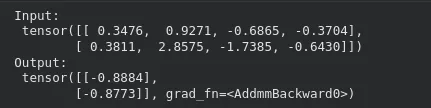
In this arrangement, SoftPlus activation is used so that the values passed from the first layer to the second layer are non-negative. Replacement of SoftPlus by the existing model may not require any other structural changes. It is only important to remember that SoftPlus can be slightly slower in training and requires more calculations than ReLU.
The last layer can also be implemented with SoftPlus when there are positive values that a model should generate as output, for example scale parameters or positive regression objectives.
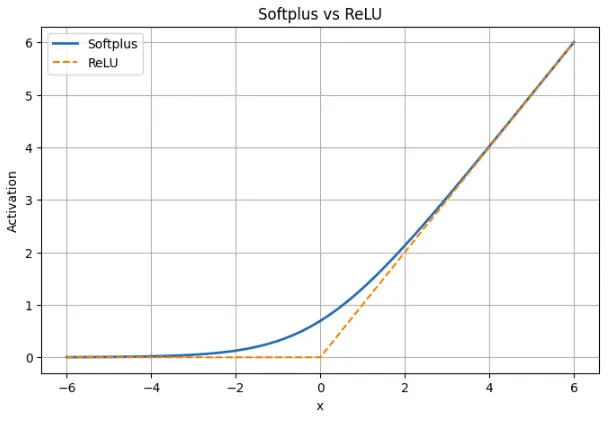
SoftPlus vs ReLU: Comparison Table
| aspect | softplus | ReLU |
|---|---|---|
| Definition | f(x) = ln(1 + ex, | f(x) = max(0, x) |
| size | smooth transition in all x | sharp turn at x = 0 |
| behavior for x < 0 | small positive output; never reaches zero | output is absolutely zero |
| Example at x = -2 | softplus ≈ 0.13 | ReLU = 0 |
| near x = 0 | Smooth and varied; value ≈ 0.693 | not differentiable at 0 |
| behavior for x > 0 | Almost linear, closely matches ReLU | linear with slope 1 |
| Example at x = 5 | softplus ≈ 5.0067 | ReLU = 5 |
| shield | Always non-zero; The derivative is sigmoid(x) | Zero for x < 0, undefined at 0 |
| Danger of dead neurons | nobody | Possible for negative input |
| rarity | does not produce exact zero | produces real zero |
| training effect | Steady gradient flow, smooth update | Simple but may stop learning for some neurons |
An analog of ReLU is SoftPlus. This is ReLU with very large positive or negative inputs but with the vertices at zero removed. This prevents dead neurons because the gradient does not go to zero. This comes at the cost that SoftPlus does not generate true zeros which means it is not as sparse as ReLU. SoftPlus provides more comfortable training dynamics in practice, but ReLU is still used because it is faster and simpler.
Benefits of using SoftPlus
SoftPlus has some practical benefits that make it useful in some models.
- Everywhere is simple and different
There are no sharp corners in SoftPlus. This is completely different for each input. This helps maintain gradients which may ultimately make adaptation a little easier as damage is slowed.
- protects against dead neurons
ReLU can stop updates when the neuron receives continuous negative input, because the gradient will be zero. SoftPlus does not return exact zero values at negative numbers and thus all neurons remain partially active and updated on the gradient.
- reacts more favorably to negative input
SoftPlus does not filter out negative inputs by generating a zero value like ReLU, but instead generates a small positive value. This allows the model to retain a portion of the information from negative signals instead of losing all of it.
In short, SoftPlus keeps gradients flowing, prevents dead neurons and offers smooth behavior used in some architectures or tasks where consistency is important.
Limitations and trade-offs of SoftPlus
SoftPlus also has some disadvantages that limit the frequency of its use.
- more expensive to calculate
SoftPlus uses exponential and logarithmic operations which are slower than SimplePlus max(0, x) Of ReLU. This additional overhead can be clearly felt on larger models because ReLU is highly optimized on most hardware.
- no true rarity
ReLU produces true zeros on negative examples, which can save computing time and sometimes aid regularization. SoftPlus does not give true zeros and hence not all neurons are always inactive. This eliminates the risk of dead neurons as well as the efficiency benefits of sparse activations.
- Gradually slow down the convergence of deep networks
ReLU is commonly used to train deep models. It has a sharp cutoff and linear positive region which can force learning. SoftPlus is smoother and may have slower updates, especially in very deep networks where the differences between layers are small.
To summarize, SoftPlus has good mathematical properties and avoids problems such as dead neurons, but these advantages do not always translate into better results in deep networks. It is best used in cases where smoothness or positive outputs are important, rather than a universal replacement for ReLU.
conclusion
SoftPlus provides an intuitive, soft alternative to ReLU for neural networks. It learns gradients, does not kill neurons and varies perfectly across the input. It is like ReLU at large values, but at zero, it behaves more like a constant than ReLU because it produces non-zero outputs and slopes. Meanwhile, it’s all about trade-offs. It is also slow to compute; It also does not generate true zeros and cannot speed up learning in deep networks as fast as ReLU. SoftPlus is more effective in models where gradients are smooth or where positive outputs are mandatory. In most other scenarios, it is a useful alternative to the default replacement of ReLU.
Frequently Asked Questions
A. SoftPlus prevents dead neurons by keeping the gradient non-zero for all inputs, providing an intuitive alternative to ReLU while behaving similarly for large positive values.
A. This is a good choice when your model benefits from smooth gradients or must output strictly positive values such as scale parameters or some regression targets.
A. It is slower to compute than ReLU, does not create sparse activations, and may converge slightly slower in deeper networks.
Login to continue reading and enjoy expertly curated content.